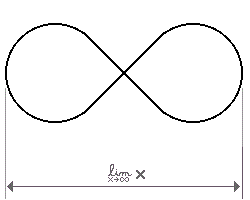Das Eineck
Ein Eineck widerspricht auf jeden Fall der allgemeinen Polygontheorie, wie schon im Thema „Innenwinkelsumme” angesprochen wurde.
„Nicht vorstellbar, wie eine geschlossene Figur mit nur einer Ecke aussehen soll!
Der Innenwinkel beträgt -180°, das widerspricht bereits der Festlegung einer Ecke.
Der Außenwinkel beträgt 540°, jedoch kann ein einzelner Winkel nicht größer als 360° sein. Noch ein Widerspruch!
Ein Eineck kann folglich nicht existieren.”
Wenn nun aber die Fläche nicht begrenzt und die Ebene nicht absolut eben sein braucht, dann gibt es doch eine Lösung.
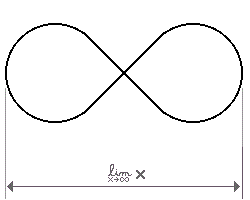
Entscheidend ist, daß sich die geraden Enden der Schleifen rechtwinklig treffen.
Es befinden sich also jeweils zwei rechte Winkel innen und nicht innen.
Aber was ist „innen”? Das negative Vorzeichen bei der Innenwinkelsumme sagt aus, daß das, was nach außen aussieht, eigentlich innen ist.
Also „innen” ist der Bereich außerhalb der Schleife. Zwei Winkel zu je 90° summieren sich zu 180° - kommt also alles hin.
Wenn noch die Außenwinkelsumme auf zwei gleiche Winkel verteilt wird, ergibt sich 270° je Winkel. Auch das ist abgreifbar.
Aber was ist jetzt „außen”? Kurz gesagt: alles, wobei die von den Schleifen eingeschlossenen Bereiche doppelt zählen,
da überlappt sich der Außenbereich nämlich selbst.