Simplex
Als Simplex wird eine geometrische Figur mit minimaler Ecken- und Kantenzahl unter Ausnutzung aller vorgegebenen Dimensionen bezeichnet.
Regelmäßige Simplices werden gerne bevorzugt, sind aber nicht zwingend.
Ab der zweiten Dimension besteht die Oberfläche aus einzelnen Dreiecken.
Die Frage, ob es negative Simplices gibt, soll hier nicht behandelt werden.
| Planfigur | Name | Dimensionen | Ecken | Kanten | Flächen | Zellen | Hyperräume
|
|---|
| · | Punkt | 0 | 1 | 0 | 0 | 0 | 0
|
| ━━ | Strecke | 1 | 2 | 1 | 0 | 0 | 0
|
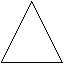 | Dreieck | 2 | 3 | 3 | 1 | 0 | 0
|
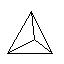 | Tetraëder | 3 | 4 | 6 | 4 | 1 | 0
|
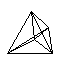 | Fünfzell | 4 | 5 | 10 | 10 | 5 | 1
|
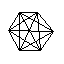 | Simplex-5 | 5 | 6 | 15 | 20 | 15 | 6
|
| | Simplex-n | n | n+1 | _n(n+1)_
2 | _n(n²-1)_
6
| _n⁴-2n³-n²+2n_
24 | _(n+1)!_
(n-4)!·5!
|