Hauptseite
Pacific (Lokomotive)
sechsachsige Dampflokomotive, alternative Bezeichnungen: 2C1, 231, 4-6-2, 3/6
Palindrom
Zeichenfolge, die in Leserichtung und entgegen der Leserichtung gleich ist
Pause (Musik)
Pentalsystem
Periode
regelmäßig wiederkehrende Abfolge
peta
π
auch „Kreiszahl” genannt, Anfangsbuchstabe des Wortes περιφέρεια
(periféreia = Kreisumfang).
Zahlenwert: 3,14159265358979...
piko
PIRL
Abkürzung für: Ponys im realen Leben
Visualisierung von Fanfiction zur Serie „My little Pony” in einer realen Umgebung
Polygon
zweidimensionale, geschlossene geometrische Figur
Im Deutschen besteht der Name aus einer Zahl und der Endung -eck.
Das paßt nur, weil hierbei Ecken- und Kantenzahl gleich sind.
siehe auch: Simplex, Quadex,
Innenwinkelsumme, Eineck
weitere Ausführungen
Polygramm
gleichbedeutend mit Sternpolygon
Potenz
Ergebnis aus der Verknüpfung einer Basis mit einem Exponenten (c=ab)
Wenn b∈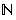 , heißt das, den Faktor a b-mal aufzuschreiben und die Mulitiplikation auszuführen.
, heißt das, den Faktor a b-mal aufzuschreiben und die Mulitiplikation auszuführen.
Die weiteren Potenzregeln bauen darauf auf.
Prairie
fünfachsige Dampflokomotive, alternative Bezeichnungen: 1C1, 131, 2-6-2, 3/5
Prime
reine Prime: einzelner Ton einer Tonleiter, mit sich selbst verglichen
chromatische Prime: entspricht in etwa der kleinen Sekunde
Primzahl
Zahl, die nur durch 1 und sich selbst ganzzahlig teilbar ist. Genau genommen wird sogar nur die natürliche Zahlenmenge betrachtet!
Zur Ermittlung von Primzahlen kann das „Sieb des Eratosthenes” verwendet werden:
Man schreibt alle natürlichen Zahlen des zu untersuchenden Bereichs auf, streicht die 1, die nicht als Primzahl gilt (da 1 mal irgend etwas immer noch das gleiche Irgendetwas ergibt)
und streicht weiter die Zahlen aus, die keine Primzahlen sind, also alle Vielfachen der bisher gefundenen Primzahlen.
Kommt man bei (Quadratwurzel aus (höchste Zahl +1)) an, und hat man sorgfältig gearbeitet, kann man davon ausgehen, daß nun alle nicht gestrichenen Zahlen im gewählten Bereich Primzahlen sind.
Pyramidenzahl, Pentaederzahl
Die Summe aller Quadratzahlen von 1 bis n2 ergibt praktisch eine Pyramidenzahl.
Als Formel ergibt sich: z=n(n+1)(2n+1)/6 (hergeleitet aus Gleichungssystem mit 4 Unbekannten und nachträglicher Faktorisierung).
Nachtrag: Diese Beschreibung bezieht sich speziell auf eine quadratische Pyramide.
Pythagoras, Satz des ~






















































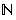 , heißt das, den Faktor a b-mal aufzuschreiben und die Mulitiplikation auszuführen.
, heißt das, den Faktor a b-mal aufzuschreiben und die Mulitiplikation auszuführen.